Understanding
This lesson helps students to use the point slope form of a line to move from graphs of proportional relationships to graph of any line.
What to look for
Student discussion may provide an opportunity to discuss why the denominator of a fraction cannot be zero.
Sample Assessment
Consider the graph of a line.
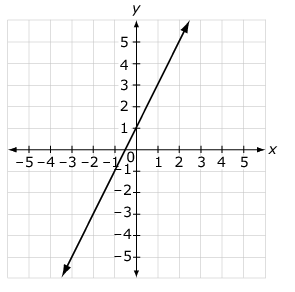
Which equation has a slope greater than the slope for the line shown?
a. \(y = 3x-1\)
b. \(y = \frac{x}{2}+4\)
c. \(y = 2x+2\)
d. \(y = \frac{x}{3}-3\)
Answer: a




